Machine Learning

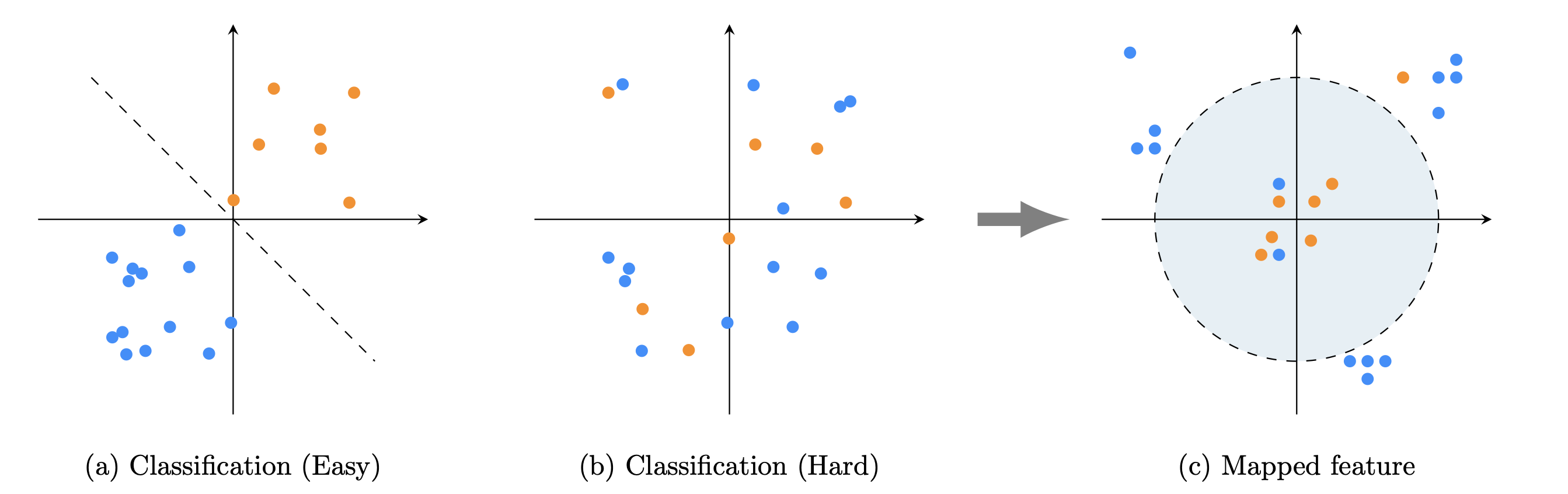
A fundamental issue in Machine Learning (ML) predictive modeling is robustness and sensitivity to data quality. Machine learning involving complex noisy observations involves a host of difficulties, including the problem of overfitting, which can give rise to highly unstable and inaccurate decision boundaries. The fundamental questions are: Does there exist a good separation of the classes in some coordinate system? How can we construct a transformation that can reveal this separation in an appropriate space?

To answer these questions we treat the data as realizations of a random field and apply the machinery of tensor product theory.