Machine Learning

A fundamental issue in Machine Learning (ML) predictive modeling is robustness and sensitivity to data quality. Machine learning involving complex noisy observations involves a host of difficulties, including the problem of overfitting, which can give rise to highly unstable and inaccurate decision boundaries. The fundamental questions are: Does there exist a good separation of the classes in some coordinate system? How can we construct a transformation that can reveal this separation in an appropriate space?

To answer these questions we treat the data as realizations of a random field and apply the machinery of tensor product theory.

Stochastic Features

Application: Alzheimer’s and cancer applications

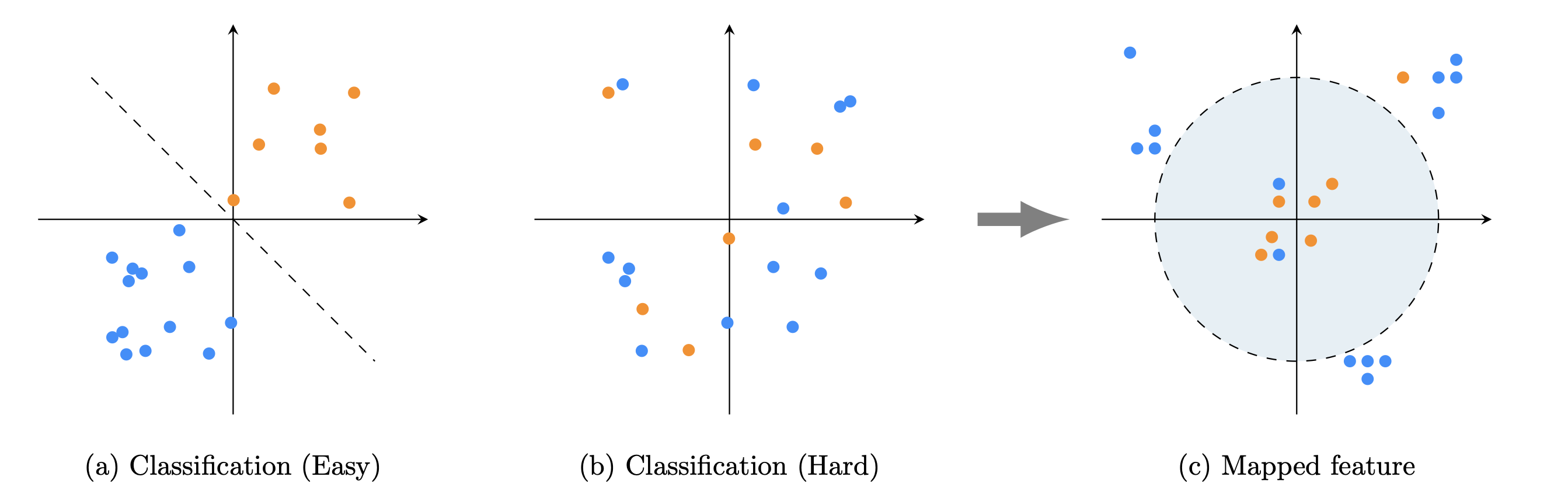
In this paper we develop a Multilevel Orthogonal Subspace (MOS) Karhunen-Loeve feature theory based on stochastic tensor spaces, for the construction of robust machine learning features. Training data is treated as instances of a random field within a relevant Bochner space. Our key observation is that separate machine learning classes can reside predominantly in mostly distinct subspaces. Using the Karhunen-Loeve expansion and a hierarchical expansion of the first (nominal) class, a MOS is constructed to detect anomalous signal components, treating the second class as an outlier of the first. The projection coefficients of the input data into these subspaces are then used to train a Machine Learning (ML) classifier. These coefficients become new features from which much clearer separation surfaces can arise for the underlying classes. Tests in the blood plasma dataset (Alzheimer's Disease Neuroimaging Initiative) show dramatic increases in accuracy. This is in contrast to popular ML methods such as Gradient Boosting, RUS Boost, Random Forest and (Convolutional) Neural Networks.

Feature Network Methods

A machine learning (ML) feature network is a graph that connects ML features in learning tasks based on their similarity. This network representation allows us to view feature vectors as functions on the network. By leveraging function operations from Fourier analysis and from functional analysis, one can easily generate new and novel features, making use of the graph structure imposed on the feature vectors. Such network structures have previously been studied implicitly in image processing and computational biology. We thus describe feature networks as graph structures imposed on feature vectors, and provide applications in machine learning. One application involves graph-based generalizations of convolutional neural networks, involving structured deep learning with hierarchical representations of features that have varying depth or complexity. This extends also to learning algorithms that are able to generate useful new multilevel features. Additionally, we discuss the use of feature networks to engineer new features, which can enhance the expressiveness of the model. We give a specific example of a deep tree-structured feature network, where hierarchical connections are formed through feature clustering and feed-forward learning. This results in low learning complexity and computational efficiency. Unlike "standard" neural features which are limited to modulated (thresholded) linear combinations of adjacent ones, feature networks offer more general feedforward dependencies among features. For example, radial basis functions or graph structure-based dependencies between features can be utilized.

Coupled VAE: Improved Accuracy and Robustness of a Variational Autoencoder

We present a coupled variational autoencoder (VAE) method, which improves the accuracy and robustness of the model representation of handwritten numeral images. The improvement is measured in both increasing the likelihood of the reconstructed images and in reducing divergence between the posterior and a prior latent distribution. The new method weighs outlier samples with a higher penalty by generalizing the original evidence lower bound function using a coupled entropy function based on the principles of nonlinear statistical coupling. We evaluated the performance of the coupled VAE model using the Modified National Institute of Standards and Technology (MNIST) dataset and its corrupted modification C-MNIST. Histograms of the likelihood that the reconstruction matches the original image show that the coupled VAE improves the reconstruction and this improvement is more substantial when seeded with corrupted images. All five corruptions evaluated showed improvement. For instance, with the Gaussian corruption seed the accuracy improves by 1014 (from 10−57.2 to 10−42.9 ) and robustness improves by 1022 (from 10−109.2 to 10−87.0 ). Furthermore, the divergence between the posterior and prior distribution of the latent distribution is reduced. Thus, in contrast to the 𝛽 -VAE design, the coupled VAE algorithm improves model representation, rather than trading off the performance of the reconstruction and latent distribution divergence.

BowSaw: Inferring Higher-Order Trait Interactions Associated With Complex Biological Phenotypes

Machine learning is helping the interpretation of biological complexity by enabling the inference and classification of cellular, organismal and ecological phenotypes based on large datasets, e.g., from genomic, transcriptomic and metagenomic analyses. A number of available algorithms can help search these datasets to uncover patterns associated with specific traits, including disease-related attributes. While, in many instances, treating an algorithm as a black box is sufficient, it is interesting to pursue an enhanced understanding of how system variables end up contributing to a specific output, as an avenue toward new mechanistic insight. Here we address this challenge through a suite of algorithms, named BowSaw, which takes advantage of the structure of a trained random forest algorithm to identify combinations of variables (“rules”) frequently used for classification. We first apply BowSaw to a simulated dataset and show that the algorithm can accurately recover the sets of variables used to generate the phenotypes through complex Boolean rules, even under challenging noise levels. We next apply our method to data from the integrative Human Microbiome Project and find previously unreported high-order combinations of microbial taxa putatively associated with Crohn’s disease. By leveraging the structure of trees within a random forest, BowSaw provides a new way of using decision trees to generate testable biological hypotheses.

CONTACT

Stochastic Machine Learning Group

QUICK LINKS

Research

Group Publications

Team

Institute - Department of Mathematics and Statistics

Privacy and Terms